En realidad el algoritmo criptográfico es el conocido como "Solitario" ('Solitaire'), pero en la novela se refieren a él con el nombre de "Pontifex" para ocultar el hecho de que se emplea una baraja de cartas.
En la novela, Enoch Root lo describe de forma general como un criptosistema que "emplea una permutación de 54 elementos como clave —¡una clave por mensaje, por supuesto!— y emplea esa permutación (que representaremos como T) para generar un flujo de clave que se añade, módulo 26, al texto llano (P), como en un cuaderno de uso único. El proceso de generar cada carácter en el flujo de clave altera T de una forma reversible pero más o menos «aleatoria»".
Lo que me recuerda mucho, también se menciona en la novela, a RC4 (ver este post donde explico este criptosistema), y, al igual que éste, 'Solitaire' es un algoritmo de cifrado simétrico (se utiliza la misma clave para cifrar y para descifrar) y de flujo ('Stream cipher').
Voy a ver si lo he entendido y para ello utilizo como base un ejemplo que figura en el sitio web de Bruce Schneier, y lo voy a desarrollar de forma análoga a lo que indiqué para RC4 en el post al que me he referido antes
En este primer ejemplo no utilizaré clave: mensaje a cifrar (M) = "AAAAA" y clave (K) = "".
Divido M en grupos de cinco letras (sólo las 26 letras mayúsculas del alfabeto inglés, de la 'A' a la 'Z') y, si hace falta, completo el último grupo de cinco con caracteres de relleno (por ejemplo: 'X').
M = "AAAAA"
El algoritmo "Solitario" ('Solitaire'), al igual que RC4, puede entenderse como compuesto por tres etapas:
1.- Inicialización de la baraja:
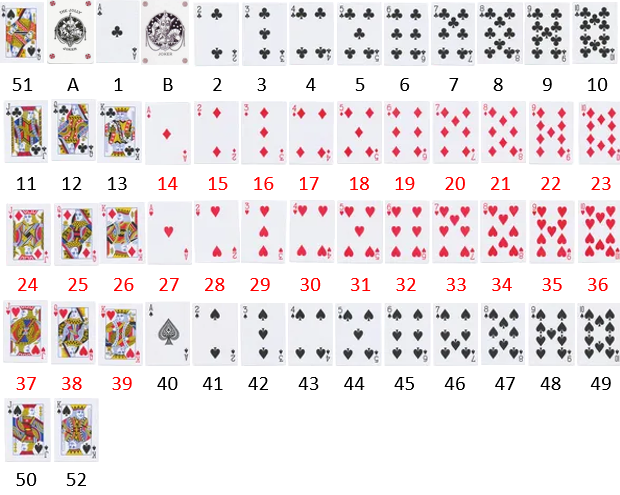
Utilizo una baraja de póquer con dos comodines ('jokers') y numero sus cartas secuencialmente del 1 al 52 (del As al Rey y con el siguiente orden de sus palos: tréboles, diamantes, corazones y picas), y a los dos comodines, que deben ser distintos, los rotulo como 'A' y 'B':
2.- Generación del flujo de clave ('key-stream') a partir de la posición inicial de la baraja y la clave secreta (K) compartida por el emisor y el receptor (como he comentado antes en este primer ejemplo no utilizo clave, y, por tanto, parto sólo de la posición inicial de la baraja).
2.1.- Busco el comodín 'A' y lo muevo debajo de la carta que tiene justo debajo (si el comodín 'A' está situado al final de la baraja lo muevo debajo de la primera
carta).
Busco el comodín 'B' y lo muevo debajo de la carta que está debajo de la que tiene justo debajo (si el comodín 'B' está situado al final de la baraja lo muevo debajo de la segunda carta de la misma y si está como anteúltima carta lo muevo debajo de la primera).
2.2.- Corto la baraja en tres partes: la primera con las cartas comprendidas entre la primera y el primer comodín que encuentro (en el ejemplo el comodín 'B'), excluido este primer comodín, la segunda con las cartas comprendidas entre el primer comodín que encuentro, incluido éste, y el segundo comodín, incluido éste, y la tercera con las cartas comprendidas entre el segundo comodín, excluido éste, y la última carta, e intercambio las partes uno y tres, o, lo que es lo mismo, intercambio las cartas que están antes del primer comodín que encuentro con las que están detrás del segundo comodín:
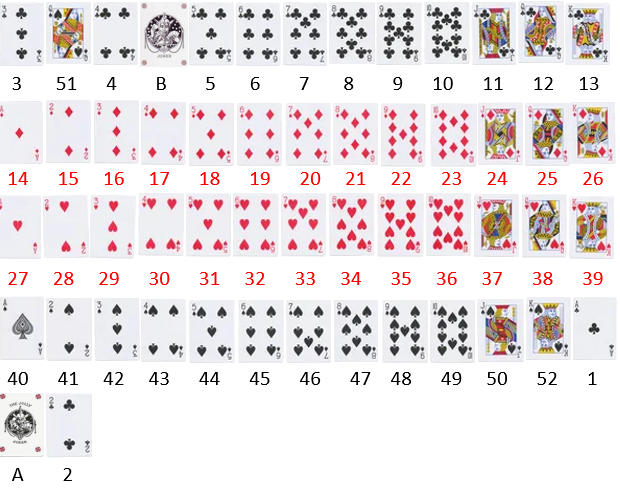
2.3.- La última carta es el AS de tréboles, por lo que muevo 1 carta (el número asignado a esa carta al inicializar la baraja. Si la última carta es un comodín la baraja no sufre cambios) del inicio de la baraja justo encima de la última carta:
2.4.- Repito los pasos anteriores de esta segunda etapa (2.1 a 2.3) hasta obtener un flujo de clave ('key-stream') de la misma longitud que el mensaje a cifrar (M), en el ejemplo hay que repetirlos 4 veces más, ya que M tiene una longitud de 5 caracteres.
- Segundo número del flujo de clave ('key-stream'):
Muevo el comodín 'A' y el 'B':
- Tercer número del flujo de clave ('key-stream'):
Muevo el comodín 'A' y el 'B':
Intercambio las cartas que están antes del primer comodín que encuentro con las que están detrás del segundo comodín:
La última carta es el As de tréboles, por lo que muevo 1 carta del inicio de la baraja justo encima de la última carta:
- Cuarto número del flujo de clave ('key-stream'):
Muevo el comodín 'A' y el 'B':
Intercambio las cartas que están antes del primer comodín que encuentro con las que están detrás del segundo comodín:
Muevo el comodín 'A' y el 'B':
- Quinto número del flujo de clave ('key-stream'):
Muevo el comodín 'A' y el 'B':
Ahora, la primer carta es el 6 de tréboles, por lo que cuento 6 cartas desde el principio de la baraja, y el quinto número del flujo de clave ('key-stream') es el número asignado a la siguiente carta al inicializar la baraja (en el ejemplo la séptima carta es el 8 de tréboles y, por tanto, 8)
Con lo que el flujo de clave ('key-stream') es: 4 49 10 24 8
3.- Cifrado:
Suma módulo 26 de los números correspondientes a cada carácter del mensaje a cifrar (M), 'A' = 1; 'B' = 2;... ; 'Z' = 26, con los correspondientes al flujo de clave ('key-stream') obtenido en la etapa anterior.
En el ejemplo:
- Primera letra del criptograma:
1ª letra del mensaje a cifrar = 'A' = 1; (1 + 4) mod 26 = 5 = 'E'.
- Segunda letra del criptograma:
2ª letra del mensaje a cifrar = 'A' = 1; (1 + 49) mod 26 = 24 = 'X'.
- Tercera letra del criptograma:
3ª letra del mensaje a cifrar = 'A' = 1; (1 + 10) mod 26 = 11 = 'K'.
- Cuarta letra del criptograma:
4ª letra del mensaje a cifrar = 'A' = 1; (1 + 24) mod 25 = 25 = 'Y'.
- Quinta letra del criptograma:
5ª letra del mensaje a cifrar = 'A' = 1; (1 + 8) mod 25 = 9 = 'I'.
Con lo que obtengo el siguiente criptograma (C): EXKYI
Y para descifrar bastará con restar módulo 26 a los números correspondientes a cada carácter del criptograma (C), 'A' = 1; 'B' = 2;... ; 'Z' = 26, los correspondientes al flujo de clave ('key-stream').
En el ejemplo:
- Primera letra del texto en claro:
1ª letra del criptograma = 'E' = 5; (5 - 4) mod 26 = 1 = 'A'.
- Segunda letra del texto en claro:
2ª letra del criptograma = 'X' = 24; (24 - 49) mod 26 = 1 = 'A'.
- Tercera letra del texto en claro:
3ª letra del criptograma = 'K' = 11; (11 - 10) mod 26 = 1 = 'A'.
- Cuarta letra del texto en claro:
4ª letra del criptograma = 'Y' = 25; (25 - 24) mod 26 = 1 = 'A'.
- Quinta letra del texto en claro:
5ª letra del criptograma = 'I' = 9; (9 - 8) mod 26 = 1 = 'A'.
Con lo que obtengo el siguiente mensaje descifrado (M): AAAAA
En un próximo post pondré un ejemplo utilizando una clave, lo que, lógicamente, es fundamental, ya que la seguridad de cualquier criptosistema reside en ella.
Comentarios
Publicar un comentario