Ir al contenido principal

Criptografía (CCLXXXIII): Ataque de intermediario al Intercambio de clave de Diffie-Hellman en python

Imagen
De

Continúo poniendo scripts de programación en python para automatizar tareas que tengan relación con la criptografía.

Ya puse una entrada en la que expliqué el funcionamiento del protocolo criptográfico para el intercambio de clave de Diffie-Hellman, que se utiliza en canales de comunicación inseguros, como puede ser Internet, para salvaguardar el secreto de la clave si las comunicaciones entre las partes son interceptadas por un tercero.

Asimismo, en esta entrada expliqué en que consiste el ataque de intermediario (MitM, por las siglas en inglés de 'Man in the Middle') aplicado a este protocolo cuando se realiza sin autenticación, y en esta entrada incluyo un script en python para implementar este ataque.

El script simula el intercambio de clave, por ejemplo: una clave de sesión para ser utilizada en el cifrado y descifrado de mensajes mediante AES, entre A y B, de la misma manera que el que puse en este post, pero añade la participación de un atacante (C) que se interpone en las comunicaciones entre A y B.

Para que el script funcione se necesita importar los dos siguientes módulos en el programa principal, que se encargarán, respectivamente, de la generación de un número primo 'p' de 2.048 bits y de realizar las operaciones de exponenciación modular de forma eficiente.

#!/usr/bin/env python
# -*- coding: utf-8 -*-

# GENERACIÓN DE UN NÚMERO PRIMO ALEATORIO:
#
# Generación de un número primo aleatorio a partir de un número de b bits.
#
# http://mikelgarcialarragan.blogspot.com/

from sympy import primerange, prime 
from random import randint, getrandbits

def test_miller_rabin(n,k):
# n = número natural mayor que 1 e impar del que queremos conocer si es primo.
# k = número de veces o rondas a ejecutar el test.
# t = indicador de que n es primo con un cierto nivel de confianza (0: primo; 1: compuesto).
# s = número de veces que 2 divide a n - 1.
    t = 0
    s = 0
    r = n - 1

    while r%2 == 0:
        s+=1
        r = r//2

    i=0 
    while i in range(0, k) and t != 1:
        a = randint(2, n - 1)
        j = 0
        y = pow(a, r, n)
        if y != 1 and y != n - 1:
            j = 1
            while y != n - 1 and t != 1 and j <= s - 1:
                y = pow(y, 2, n)
                if y == 1:
                    t = 1
                else:
                    j = j + 1
            if y != n -1:
                t = 1
        i = i + 1

    if t == 0:
        return True
    else:
        return False

def generar_primo_aleatorio(b,k):
# b = número de bits que tendrá como mínimo el número primo aleatorio.
# k = número de veces o rondas a ejecutar el test de primalidad.
# Se genera un número aleatorio impar (p) de b bits.
    p = getrandbits(int(b))
    if p%2 == 0:
        p+=1

# Se crea una lista con los primeros 2048 números primos, para descartar rápidamente aquellos
# candidatos no primos, es decir, aquellos que son divisibles por alguno de los números primos
# integrantes de esta lista.
    primeros_2048_primos = list(primerange(prime(2048 + 1)))

# Se realizan las comprobaciones tendentes a verificar si el candidato es primo con un cierto
# nivel de confianza.
    puede_ser_primo = False
    while not puede_ser_primo:
        puede_ser_primo = True
        for primo in primeros_2048_primos:
            if p%primo == 0:
                puede_ser_primo = False
                break
        # Si el candidato supera la primera criba, es decir no es divisible entre ninguno de los primeros
        # 2048 números primos, entonces se le somete al test de primalidad de Miller-Rabin.
        if puede_ser_primo:
            if not test_miller_rabin(p,int(k)):
                puede_ser_primo = False
        # Si el candidato no supera la primera criba, es decir es divisible entre alguno de los primeros
        # 2048 números primos o no supera el test de primalidad de Miller-Rabin, entonces se incrementa
        # al candidato en dos unidades y se vuelve a comprobar si el nuevo candidato puede ser primo.
        if not puede_ser_primo:
                p+=2

    return p


#!/usr/bin/env python
# -*- coding: utf-8 -*-

# ALGORITMO DE EXPONENCIACIÓN MODULAR RÁPIDA:
#
# Algoritmo utilizado en operaciones de exponenciación modular
# con números muy grandes con objeto de hacerlas de forma
# más eficiente.
#
# http://mikelgarcialarragan.blogspot.com/

def exp_modular_rapida(b, e, m):
    c = 1
    e = bin(e)[2:]

    for i in range(0, len(e)):
        c = pow(c, 2, m)
        if e[i]=="1":
            c = c*b%m

    return c

El script es el siguiente:

#!/usr/bin/env python
# -*- coding: utf-8 -*-

# ATAQUE DE INTERMEDIARIO ('MAN IN THE MIDDLE') AL INTERCAMBIO DE CLAVE DE DIFFIE-HELLMAN:
#
# Ataque de intermediario (MitM) al Protocolo de intercambio de clave de Diffie-Hellman cuando éste se realiza sin autenticación.
#
# http://mikelgarcialarragan.blogspot.com/

import hashlib
import primo_aleatorio
from exponenciacion_modular_rapida import exp_modular_rapida

def main():
# MENÚ:
# Se presenta el menú para que se seleccione una opción.
    salir = False
    while not salir:
        print ("")
        print ("*** MENÚ *****************************************")
        print ("1. Ataque MitM al protocolo Diffie-Hellman.")
        print ("2. Salir.")
        print ("")
        opcion = input("Por favor, seleccione una opción: ")
        if opcion == "1":
            print ("")
            print ("--- ATAQUE DE INTERMEDIARIO ('MAN IN THE MIDDLE') AL INTERCAMBIO DE CLAVE DE DIFFIE-HELLMAN:")
            print ("*** A genera un número primo aleatorio 'p' de 2.048 bits y escoge 'g' = 5")
            p = primo_aleatorio.generar_primo_aleatorio(2048,5)
            g = 5
            print ("[+] Número primo aleatorio 'p' generado:", p)
            print ("[+] Número 'g' escogido:", g)
            print ("*** A envía a C, que se ha interpuesto en las comunicaciones entre A y B, el número primo aleatorio 'p' y 'g'")
            print ("*** C envía a B, el número primo aleatorio 'p' y 'g' que ha recibido de A")
            print ("*** A introduce una frase de contraseña de la que se calcula el hash SHA-256 para obtener su número secreto 'a'")
            frase_password = ""
            while frase_password == "":
                frase_password = input('Por favor, introduzca su frase de contraseña: ')
                if frase_password != "":
                    a = (hashlib.sha256(frase_password.encode()).digest()).hex()
                    print ("[+] Número secreto de A (hexadecimal), 'a':", a)
                    print ("*** A envía a C, creyendo que se lo envía a B, el resultado de g^a mod p")
                    print ("*** C introduce una frase de contraseña de la que se calcula el hash SHA-256 para obtener su propio número secreto 'c'")
                    frase_password = ""
                    while frase_password == "":
                        frase_password = input('Por favor, introduzca su frase de contraseña: ')
                        if frase_password != "":
                            c = (hashlib.sha256(frase_password.encode()).digest()).hex()
                            print ("[+] Número secreto del atacante C (hexadecimal), 'c':", c)
                            print ("*** C envía a B, que cree que se lo ha enviado A, el resultado de g^c mod p")
                            print ("*** B introduce una frase de contraseña de la que se calcula el hash SHA-256 para obtener su número secreto 'b'")
                            frase_password = ""
                            while frase_password == "":
                                frase_password = input('Por favor, introduzca su frase de contraseña: ')
                                if frase_password != "":
                                    b = (hashlib.sha256(frase_password.encode()).digest()).hex()
                                    print ("[+] Número secreto de B (hexadecimal), 'b':", b)
                                    print ("*** B envía a C, creyendo que se lo envía a A, el resultado de g^b mod p")
                                    print ("*** C envía a A, que cree que se lo ha enviado B, el resultado de g^c mod p")
                                    print ("*** A calcula la clave de sesión que cree que va a compartir con B, pero que realmente va a compartir con C: k = (g^c mod p)^a mod p")
                                    ka = exp_modular_rapida(exp_modular_rapida(g, int(c,16), p), int(a,16), p)
                                    print ("[+] Clave de sesión compartida ('k') calculada por A, que cree que va a compartir con B pero realmente lo va a hacer con el atacante (C):", ka)
                                    print ("*** B calcula la clave de sesión que cree que va a compartir con A, pero que realmente va a compartir con C:  k = (g^c mod p)^b mod p")
                                    kb = exp_modular_rapida(exp_modular_rapida(g, int(c,16), p), int(b,16), p)
                                    print ("[+] Clave de sesión compartida ('k') calculada por B, que cree que va a compartir con A pero realmente lo va a hacer con el atacante (C):", kb)
                                    print ("*** C calcula la clave de sesión que va a compartir de forma ilegítima con A: k = (g^a mod p)^c mod p")
                                    kca = exp_modular_rapida(exp_modular_rapida(g, int(a,16), p), int(c,16), p)
                                    print ("[+] Clave de sesión compartida ('k') calculada por C para suplantar a B de forma ilegítima en las comunicaciones con A:", kca)
                                    print ("*** C calcula la clave de sesión que va a compartir de forma ilegítima con B: k = (g^b mod p)^c mod p")
                                    kcb = exp_modular_rapida(exp_modular_rapida(g, int(b,16), p), int(c,16), p)
                                    print ("[+] Clave de sesión compartida ('k') calculada por C para suplantar a A de forma ilegítima en las comunicaciones con B:", kcb)
                                else:
                                    print ("*** ERROR: Por favor, introduzca su frase de contraseña.")
                        else:
                            print ("*** ERROR: Por favor, introduzca su frase de contraseña.")
                else:
                    print ("*** ERROR: Por favor, introduzca su frase de contraseña.")
        elif opcion == "2":
            print ("*** FIN ******************************************")
            salir = True
        else:
            print ("*** ERROR: Opción no válida.")

if __name__ == '__main__':
    main()

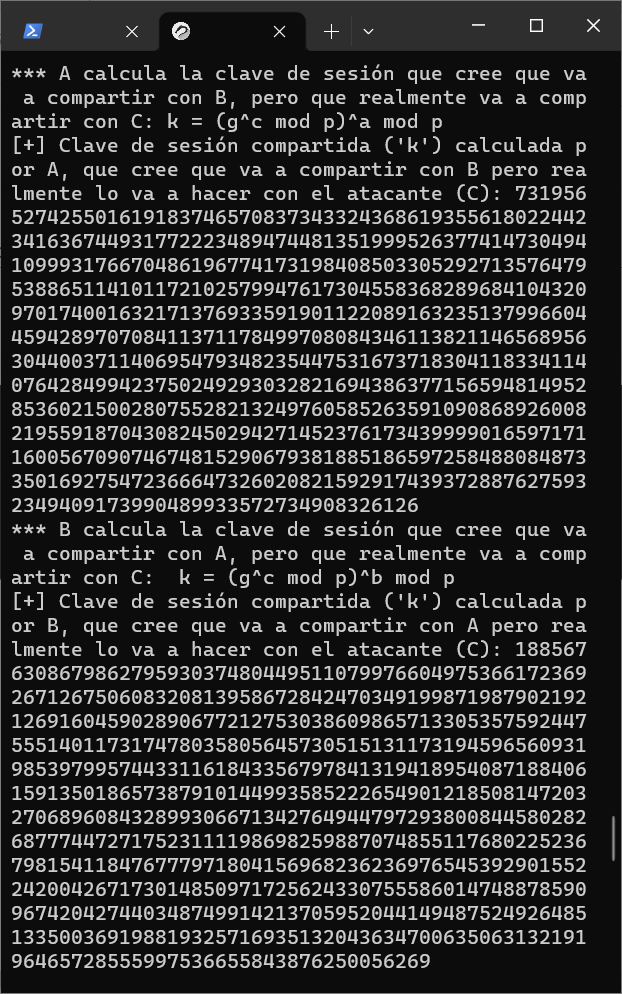
Lo ejecuto:

Tal y como decía en este post y se puede ver en las dos últimas imágenes, A y B realmente comparten la clave de sesión ('k') con C y no entre ellos, y, por tanto, cuando C reciba un mensaje cifrado de A con la clave de sesión que cree compartir con B cuando realmente la comparte con C, éste lo descifrará, es decir, tendrá acceso a su contenido, y, además, se lo enviará a B para que no se dé cuenta de que el mensaje ha sido interceptado y leído, nótese que si lo desea, además, podrá modificarlo a su entera conveniencia y volver a cifrarlo con la clave que comparte con B, y B lo descifrará con la clave de sesión que cree compartir con A cuando realmente la comparte con C, y viceversa cuando C reciba un mensaje cifrado de B.

Sus comunicaciones cifradas se encuentran totalmente comprometidas, pudiendo el atacante no sólo tener acceso a su contenido sino también modificarlas a conveniencia, y lo peor de todo es que ni siquiera se dan cuenta de que han sido hackeados.

Quizás también te interese:

Etiquetas:

Comentarios

Publicar un comentario

Entradas populares de este blog

Criptografía (I): cifrado Vigenère y criptoanálisis Kasiski

De
Hace unos días mi amigo Iñaki Regidor ( @Inaki_Regidor ), a quien dedico esta entrada :), compartió en las redes sociales un post titulado "Criptografía: el arte de esconder mensajes"  publicado en uno de los blogs de EiTB . En ese post se explican ciertos métodos clásicos para cifrar mensajes , entre ellos el cifrado de Vigenère , y , al final del mismo, se propone un reto consistente en descifrar un mensaje , lo que me ha animado a escribir este post sobre el método Kasiski  para atacar un cifrado polialfabético ( conociendo la clave descifrar el mensaje es muy fácil, pero lo que contaré en este post es la forma de hacerlo sin saberla ). El mensaje a descifrar es el siguiente: LNUDVMUYRMUDVLLPXAFZUEFAIOVWVMUOVMUEVMUEZCUDVSYWCIVCFGUCUNYCGALLGRCYTIJTRNNPJQOPJEMZITYLIAYYKRYEFDUDCAMAVRMZEAMBLEXPJCCQIEHPJTYXVNMLAEZTIMUOFRUFC Como ya he dicho el método de Vigenère es un sistema de sustitución polialfabético , lo que significa que, al contrario que en un sistema de
105 comentarios
Leer más

¿Qué significa el emblema de la profesión informática? (I)

De
Todas o muchas profesiones tienen un emblema que las representa simbólicamente y en el caso de la  informática: " es el establecido en la resolución de 11 de noviembre de 1977  para las titulaciones universitarias superiores de informática, y  está constituido por una figura representando en su parte central  un  núcleo toroidal de ferrita , atravesado por  hilos de lectura,  escritura e inhibición . El núcleo está rodeado por  dos ramas : una  de  laurel , como símbolo de recompensa, y la otra, de  olivo , como  símbolo de sabiduría. La  corona  será la  de la casa real  española,  y bajo el escudo se inscribirá el acrónimo de la organización. ". Veamos los diferentes elementos tomando como ejemplo el emblema del COIIE/EIIEO (Colegio Oficial de Ingenieros en Informática del País Vasco/ Euskadiko Informatikako Ingeniarien Elkargo Ofiziala ) . Pero no sólo el COIIE/EIIEO adopta el emblema establecido en dicha resolución, sino que éste se adopta también como im
Publicar un comentario
Leer más

Criptografía (XXIII): cifrado de Hill (I)

De
En este post me propongo explicar de forma comprensible lo que he entendido sobre el cifrado de Hill , propuesto por el matemático Lester S. Hill , en 1929, y que se basa en emplear una matriz como clave  para cifrar un texto en claro y su inversa para descifrar el criptograma correspondiente . Hay tres cosas que me gustan de la criptografía clásica, además de que considero que ésta es muy didáctica a la hora de comprender los sistemas criptográficos modernos: la primera de ellas es que me "obliga" a repasar conceptos de matemáticas aprendidos hace mucho tiempo y, desgraciadamente, olvidados también hace demasiado tiempo, y, por consiguiente, que, como dice  Dani , amigo y coautor de este blog, me "obliga" a hacer "gimnasia mental"; la segunda es que, en la mayoría de las ocasiones, pueden cifrarse y descifrase los mensajes, e incluso realizarse el criptoanálisis de los criptogramas, sin más que un simple lápiz y papel, es decir, para mi es como un pasat
5 comentarios
Leer más