Cuadrados mágicos (V): Solución Reto 5

Solución al quinto reto sobre cuadrados mágicos y ajedrez que he puesto recientemente en este blog.

El enunciado del reto decía lo siguiente: De forma análoga que con el problema de las 8 reinas, el problema del caballo se puede generalizar para aplicarlo a un tablero de n x n casillas, de forma que un caballo colocado en una posición cualquiera del mismo pase por todas ellas una sola vez.

A la casilla en la que se sitúe inicialmente el caballo se le asignará el valor 1 y, tras cada uno de sus movimientos, a la casilla de destino se le asignará el número entero consecutivo al de la casilla de origen.

Dicho lo anterior: ¿Cuántos cuadrados de orden menor o igual que 4 construidos en base a soluciones del problema del caballo son cuadrados mágicos?. ¡Ojo, que la pregunta puede tener trampa! ;).

Solución: En cuadrados de orden menor o igual a 3 la pregunta se responde de forma inmediata, ya que es muy fácil observar que:

- Tablero de orden 1 (cuadrado de 1 fila x 1 columna):

Evidentemente, al colocarse el caballo en la única casilla existente éste pasa por todas las del tablero una única vez, y, además, el cuadrado obtenido es un cuadrado mágico. Una solución trivial a este reto, pero solución al fin y al cabo :).

- Tablero de orden 2 (cuadrado de 2 filas x 2 columnas):

También resulta evidente que, después de colocar el caballo en cada una de las 4 posiciones iniciales existentes, es imposible moverlo, por lo que nunca podrá pasar por todas las casillas del tablero y, por tanto, es imposible crear un cuadrado en base a una solución del problema del caballo.

- Tablero de orden 3 (cuadrado de 3 filas x 3 columnas):

Otra vez es evidente que es imposible crear un cuadrado en base a una solución del problema del caballo, ya que, después de colocar el caballo en la casilla central es imposible moverlo, y si se coloca en cualquiera de las otras 8 posibles posiciones iniciales es imposible pasar por la casilla central.

Lo anterior es muy fácilmente comprobable si se prueban manualmente todos los recorridos de un caballo en una tablero de 3 x 3 (recorrido: secuencia de saltos, sin repetir casillas por las que ya se ha pasado, desde una casilla inicial hasta otra final desde la cual no se puede realizar otro salto), pero creo que otra forma de verlo para concluir lo mismo es que, tal y como se muestra en la figura siguiente y considerando también como un recorrido la colocación del caballo en la casilla central, sólo hay 3 posibilidades esenciales para los recorridos del caballo en un tablero de orden 3; el resto se obtienen por rotaciones o simetrías (reflejos) de las dos últimas:

Es decir, ninguno de los dos últimos recorridos que se muestran en la figura anterior, ni del resto de recorridos posibles (todos ellos se obtienen a partir de éstos por rotación o reflejo; 14 recorridos más), pasan por la casilla central; es más, todos ellos tienen un tamaño (número de casillas por las que pasan) de 8. 

Para cuadrados de orden 4 la pregunta no es tan fácil de responder a simple vista o manualmente, pero voy a intentarlo sin acudir a la programación.

- Tablero de orden 4 (cuadrado de 4 filas x 4 columnas):

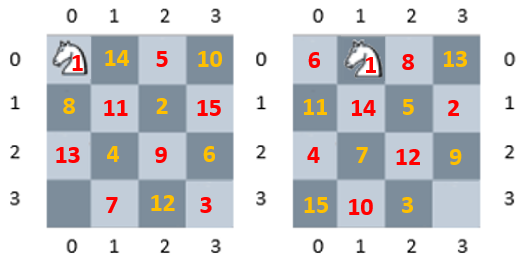
Tras múltiples intentos, tomando como posición inicial del caballo diversas casillas del tablero, no consigo obtener de forma manual ninguna solución al problema del caballo; lo máximo que consigo son recorridos de tamaño 15 (número de casillas por las que se pasa), nunca de 16. El número de recorridos de tamaño 15 obtenidos parece bastante importante, pero muchos de ellos se obtienen por rotación o simetría de otros, con lo que recorridos de tamaño 15 esenciales no hay tantos. Un ejemplo de éstos últimos serían los siguientes:

Por todo ello y aún a riego de equivocarme, concluyo que es imposible pasar por las 16 casillas del tablero sin repetir ninguna de ellas, siempre queda 1 por visitar, es decir, no existe ninguna solución al problema del caballo en un tablero de orden 4.

No obstante, ya que esto no pasa de ser una intuición me propongo demostrarlo en un próximo reto, aunque para ello tendré que recurrir a la programación.

Ya decía yo que la pregunta a este reto podía tener trampa ;), porque el único cuadrado mágico que se puede construir en base a soluciones del problema del caballo es el correspondiente a un tablero de orden 1 (1 única casilla; cuadrado posiblemente no considerado por muchos de los que hayan intentado resolver el reto por tratarse de una solución trivial), y porque para los cuadrados de orden 2, 3 y 4 simplemente no existe ninguna solución a dicho problema y, por tanto, no se puede construir ningún cuadrado en base a ninguna de ellas, ni mágico ni no mágico.

Por tanto, la respuesta a este resto es que, para los tableros de orden menor o igual a 4, únicamente se puede construir 1 cuadrado mágico en base a soluciones del problema del caballo, el cuadrado mágico de orden 1. 

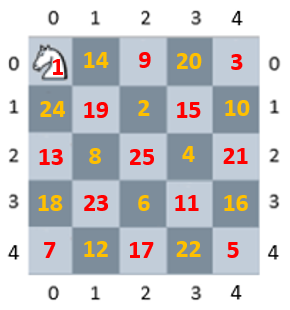
Y, ¿Qué pasaría si a la pregunta de este reto se hubieran añadido los cuadrados de orden 5? En ese caso: ¿Cuántos cuadrados de orden 5 construidos en base a soluciones del problema del caballo son cuadrados mágicos? Pues, sinceramente, no lo sé. Lo único que sé es que el número de recorridos aumenta de forma exponencial a medida que aumenta el orden del tablero y que sí existen soluciones al problema del caballo en un tablero de orden 5, ya que manualmente he obtenido una muy rápidamente:

Ahora bien, ni idea de si en base a las soluciones existentes en un tablero de orden 5 se pueden crear cuadrados mágicos (desde luego, el anterior no lo es), pero me propongo averiguarlo, y, como no tengo ni capacidad ni talento para otra cosa, utilizaré la fuerza bruta mediante un pequeño programa (ver el siguiente reto que voy a proponer a los lectores de este blog y que, como he dicho antes, también me servirá para ratificar lo intuido sobre la inexistencia de soluciones al problema del caballo en un tablero de orden 4).

******** PRÓXIMO RETO
Reto 6:   "Los cuadrados mágicos y el ajedrez (VI)".