Solución al tercer reto sobre cuadrados mágicos y ajedrez que he puesto recientemente en este blog.
El enunciado del reto decía lo siguiente: Se pide construir un cuadrado mágico de orden 4, 4 filas y cuatro columnas, normal (que contenga todos los números naturales desde el 1 hasta n2, en este caso del 1 al 16) y en el que se "escondan" todas las posibles soluciones al problema de las 4 reinas, es decir, que la suma de las casillas del cuadrado donde se ubicarían las 4 reinas de cada solución dé como resultado su constante mágica, n(n2+1)/2 = 4(17)/2=34.
Quien haya visitado la Wikipedia a través del enlace anterior ya sabrá que el número de soluciones es 2, pero: ¿Cuáles son?.
Esas 2 soluciones se pueden obtener muy fácilmente de forma manual, pero aprovechando el script de python que cree para resolver el reto anterior, adaptado al problema de las 4 reinas:
def busqueda_exhaustiva_soluciones(f):
#------------------------------------------------------------
# Busca todas las soluciones al problema de las 4 reinas.
#------------------------------------------------------------
#
global s
c=0
while c<4:
if not casilla_amenazada(f,c):
Dama[f]=c
if f==3:
s+=1
print('[+] Encontrada solución',s,'al problema de las 4 Damas:',Dama)
else:
busqueda_exhaustiva_soluciones(f+1)
c+=1
def casilla_amenazada(f,c):
#------------------------------------------------------------
# Verifica si una casilla está amenazada.
#------------------------------------------------------------
#
i=0
while i<f:
if Dama[i]==c or i-Dama[i]==f-c or i+Dama[i]==f+c:
return True
i=i+1
return False
#
#============================================
# SOLUCIÓN RETO 3: "LOS CUADRADOS MÁGICOS Y EL AJEDREZ (III)".
#============================================
#
global s
f=0
Dama=[5,5,5,5]
#
# Busca todas las soluciones al problema de las 4 reinas.
#
s=0
busqueda_exhaustiva_soluciones(f)
print('--- Total de soluciones encontradas al problema de las 4 Damas:',s)
Veo que, efectivamente, hay sólo 2 soluciones y que éstas son:
Como se observa en la figura anterior, además, sólo hay 1 solución esencial, ya que una se obtiene por simetría (reflejo) de la otra (doblar el tablero por la mitad, tanto por el eje horizontal - filas - como vertical - columnas -) y viceversa.
Conocidas ya todas las posibles soluciones, comienzo a construir el cuadrado mágico de 4x4 que las contenga utilizando el método más comúnmente empleado para la construcción de cuadrados mágicos de orden par:
- En primer lugar, dispongo sobre el tablero (cuadrado de 4 filas y 4 columnas), de izquierda a derecha y de arriba a abajo, es decir, completándolo por filas, los números del 1 al 16, de forma consecutiva y sin repetir ninguno de ellos, de la siguiente manera:
- Después, manteniendo los números dispuestos en el subcuadrado central de orden n/2 (en nuestro caso 4/2 = 2) y los cuatro subcuadrados de las esquinas de orden n/4 (en nuestro caso 4/4 = 1), giro el resto de números 180º respecto del centro del cuadrado, o, lo que es lo mismo, los recoloco en orden decreciente, de la siguiente manera:
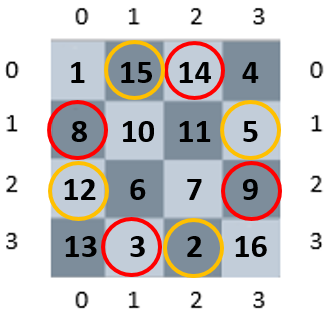
Y ya tengo un cuadrado mágico de constante mágica 34, pero es que, además, si coloco las dos soluciones al problema de las 4 reinas en sus respectivas casillas (círculo rojo y anaranjado, respectivamente) y sumo las casillas correspondientes a cada solución el resultado también es 34, es decir, esas soluciones se "esconden" en este cuadrado mágico.
3 + 5 + 12 + 14 = 34
2 + 8 + 9 + 15 = 34
Por tanto, ya he obtenido un cuadrado mágico que da solución a este reto, pero voy a ver cuántos puedo obtener de forma manual en muy poco tiempo.
A partir del cuadrado mágico obtenido como solución:
- Intercambio la primera fila (fila 0) con la cuarta (fila 3):
15 + 5 + 12 + 2 = 34
14 + 8 + 9 + 3 = 34
- Intercambio la segunda fila (fila 1) con la tercera (fila 2):
3 + 9 + 8 + 14 = 34
2 + 12 + 5 + 15 = 34
- Intercambio la primera columna (columna 0) con la cuarta (columna 3):
3 + 8 + 9 + 14 = 34
2 + 5 + 12 + 15 = 34
- Intercambio la segunda columna (columna 1) con la tercera (columna 2):
2 + 5 + 12 + 15 = 34
3 + 8 + 9 + 14 = 34
- Intercambio la primera fila (fila 0) con la cuarta (fila 3) y la primera columna (columna 0) con la cuarta (columna 3):
15 + 8 + 9 + 2 = 34
14 + 5 + 12 + 3 = 34
- Intercambio la segunda fila (fila 1) con la tercera (fila 2) y la primera columna (columna 0) con la cuarta(columna 3):
3 + 12 + 5 + 14 = 34
2 + 9 + 8 + 15 = 34
- Intercambio la primera fila (fila 0) con la cuarta (fila 3) y la segunda columna (columna 1) con la tercera (columna 2):
14 + 5 + 12 + 3 = 34
15 + 8 + 9 + 2 = 34
- Intercambio la segunda fila (fila 1) con la tercera (fila 2) y la segunda columna (columna 1) con la tercera (columna 2):
2 + 9 + 8 + 15 = 34
3 + 12 + 5 + 14 = 34
- Intercambio la primera fila (fila 0) con la cuarta (fila 3), la primera columna (columna 0) con la cuarta (columna 3) y la segunda fila (fila 1) con la tercera (fila 2):
15 + 12 + 5 + 2 = 34
14 + 9 + 8 + 3 = 34
Por cierto, ¿A qué me suena este cuadrado mágico (última línea: 4, 15, 14, 1)? Es el cuadrado mágico de Alberto Durero.
Por lo que ya he aprendido otra cosa :): las dos soluciones al problema de las 4 reinas se "esconden" en el cuadrado mágico de Alberto Durero.
- Intercambio la primera fila (fila 0) con la cuarta (fila 3), la segunda columna (columna 1) con la tercera (columna 2) y la segunda fila (fila 1) con la tercera (fila 2):
14 + 9 + 8 + 3 = 34
15 + 12 + 5 + 2 = 34
- Intercambio la primera fila (fila 0) con la cuarta (fila 3), la primera columna (columna 0) con la cuarta (columna 3) y la segunda columna (columna 1) con la tercera (columna 2):
14 + 8 + 9 + 3 = 34
15 + 5 + 12 + 2 = 34
- Intercambio la segunda fila (fila 1) con la tercera (fila 2), la primera columna (columna 0) con la cuarta (columna 3) y la segunda columna (columna 1) con la tercera (columna 2):
2 + 12 + 5 + 15 = 34
3 + 9 + 8 + 14 = 34
Ya decía yo que este reto era "Fácil", lo que creo que queda más que demostrado con los 13 cuadrados mágicos normales construidos en muy poco tiempo que cumplen los requisitos de este desafío, pero hay muchos más: ¿Cuántos y cuáles?. Asunto que dejo para el siguiente reto que voy a proponer a los lectores de este blog.
******** PRÓXIMO RETO
Reto 4: "Los cuadrados mágicos y el ajedrez (IV)".
Reto 4: "Los cuadrados mágicos y el ajedrez (IV)".



















Comentarios
Publicar un comentario