Como se ve en la figura anterior, la clave de sesión (la clave con la que se ha cifrado el texto en claro), se descifra utilizando la clave privada del receptor (criptografía asimétrica), que es el único que la posee y, por tanto, el único que puede descifrarla, y posteriormente se descifra el criptograma o texto en claro cifrado mediante la clave de sesión (criptografía simétrica).
Tal y como indique en el citado post, este esquema de cifrado, además de para mantener el secreto de la comunicación (confidencialidad), sirve para garantizar al receptor que el emisor es realmente quien ha enviado el texto en claro (autenticidad: el emisor es quien dice ser) y para comprobar que no ha sido interceptado y alterado por terceros (integridad); con la característica adicional de no repudio, tanto en origen (el emisor no puede negar que creó y envió ese texto en claro) como en destino (el receptor no puede negar que lo recibió y recibió exactamente ese texto en claro).
Estos último aspectos son los que se consiguen mediante la firma digital. El emisor firmó el contenido mediante un hash o función resumen del mismo y cifró ese resumen utilizando su clave privada RSA (nótese que, evidentemente, es el único que puede hacer esto, ya que es el único que posee su clave privada). Esta operación de cifrado dota a la comunicación de las características de autenticidad del mensaje (sólo el emisor ha podido cifrar la firma digital o resumen del mensaje con su clave privada) e integridad (si el hash descifrado es igual que el hash del texto en claro descifrado que se calcula en la recepción, entonces el mensaje no ha sido modificado desde que se envió y, por tanto, su contenido es exactamente lo que el emisor envió), y las dos características anteriores (autenticidad e integridad) dan como resultado el no repudio de la comunicación.
El script que pongo a continuación implementa las operaciones de descifrado de la clave de sesión y de la firma digital mediante RSA, y el descifrado del criptograma mediante el algoritmo AES de criptografía simétrica en modo de operación CBC.
El par de claves RSA, publica y privada, para los dos usuarios participantes en la comunicación, emisor y receptor, son las mismas que las que generé mediante el script que puse en esta entrada y utilicé en el post citado al principio: clave pública emisor, clave privada emisor, clave pública receptor, clave privada receptor.
Para simular la recepción del mensaje cifrado utilizo un archivo que se ha creado tras la ejecución del script que puse en el post anterior, comunicacion.txt, y que contiene, codificada en base64, la siguiente información: la clave de sesión cifrada, el criptograma o texto en claro cifrado y la firma digital cifrada.
Asimismo, para que el script funcione se necesita importar el siguiente módulo en el programa principal, que se encargará de la exponenciación modular rápida a realizar en las operaciones de descifrado RSA, tanto de la clave de sesión como de la firma digital, para hacer éstas más eficientemente.
#!/usr/bin/env python # -*- coding: utf-8 -*- # ALGORITMO DE EXPONENCIACIÓN MODULAR RÁPIDA: # # Algoritmo utilizado en operaciones de exponenciación modular # con números muy grandes con objeto de hacerlas de forma # más eficiente. # # http://mikelgarcialarragan.blogspot.com/ def exp_modular_rapida(b, e, m): c = 1 e = bin(e)[2:] for i in range(0, len(e)): c = pow(c, 2, m) if e[i]=="1": c = c*b%m return c
El script es el siguiente:
- Script python para el descifrado y verificación de la firma digital:
#!/usr/bin/env python # -*- coding: utf-8 -*- # CIFRADO RSA: # # Descifrar y verificar firma digital utilizando el criptosistema RSA. # # http://mikelgarcialarragan.blogspot.com/ import hashlib from Crypto.Cipher import AES from Crypto.PublicKey import RSA from base64 import b64decode from exponenciacion_modular_rapida import exp_modular_rapida # CIFRADO AES (CRIPTOGRAFÍA SIMÉTRICA). def descifrar_aes(criptograma,clave): iv = criptograma[:AES.block_size] descifrar = AES.new(clave, AES.MODE_CBC, iv) texto_claro = descifrar.decrypt(criptograma[AES.block_size:]).decode() return texto_claro[:-ord(texto_claro[len(texto_claro) - 1:])] # OBTENER DATOS DE LA CLAVE RSA. def clave_rsa(fichero_pem): f_clave_rsa = open(fichero_pem, "r") datos_clave_rsa = RSA.importKey(f_clave_rsa.read()) f_clave_rsa.close() return datos_clave_rsa def main(): # MENÚ: # Se presenta el menú para que se seleccione una opción. salir = False while not salir: print ("") print ("*** MENÚ *****************************************") print ("1. Descifrar y verificar firma digital.") print ("2. Salir.") print ("") opcion = input("Por favor, seleccione una opción: ") if opcion == "1": print ("") print ("--- DESCIFRAR Y VERIFICAR FIRMA DIGITAL:") # Descifrar y verificar firma digital: se reciben la clave de sesión cifrada, # el criptograma y la firma digital cifrada. f_comunicacion = open("comunicacion.txt") datos_comunicacion = f_comunicacion.readlines() print ("[+] Clave de sesión AES cifrada (base64):", datos_comunicacion[0].rstrip()) print ("[+] Criptograma (base64):", datos_comunicacion[1].rstrip()) print ("[+] Firma digital cifrada (base64):", datos_comunicacion[2]) # Se lee la clave privada del receptor: el módulo (n), el exponente de # la clave privada (d) y el resto de datos, para descifrar la clave de sesión. datos_clave_privada = clave_rsa("private_receptor.pem") print ("[+] Clave privada del receptor:") print (" Módulo (n):", datos_clave_privada.n) print (" Exponente clave privada (d):", datos_clave_privada.d) print (" Primer número primo factor de n (p):", datos_clave_privada.p) print (" Segundo número primo factor de n (q):", datos_clave_privada.q) print (" Coeficiente CRT (inv(p) mod q):", datos_clave_privada.u) # Se descifra la clave de sesión AES con la que se cifró el texto en claro # con la clave privada del receptor (criptografía asimétrica), utilizando el # teoema chino del resto (CRT, por sus siglas en inglés). # 1.- dp = d mod (p – 1); dq = d mod (q – 1) # 2.- cp = c mod p; cq = c mod q # 3.- k1 = cp**dp mod p; k2 = cq**dq mod q # 4.- k = k1 + (((k2 - k1)*inv(p) mod q)) mod q) * p dp = datos_clave_privada.d%(datos_clave_privada.p-1) dq = datos_clave_privada.d%(datos_clave_privada.q-1) cp = int(b64decode(datos_comunicacion[0]))%datos_clave_privada.p cq = int(b64decode(datos_comunicacion[0]))%datos_clave_privada.q k1 = exp_modular_rapida(cp, dp, datos_clave_privada.p) k2 = exp_modular_rapida(cq, dq, datos_clave_privada.q) clave_sesion = k1 + (((k2 - k1)*datos_clave_privada.u)%datos_clave_privada.q) * datos_clave_privada.p print ("[+] Clave de sesión AES descifrada (hexadecimal):", hex(clave_sesion)[2:]) # Se descifra el criptograma con la clave de sesión AES (criptografía simétrica). texto_claro = descifrar_aes(b64decode(datos_comunicacion[1]),bytes.fromhex(hex(clave_sesion)[2:])) print ("[+] Texto claro descifrado con la clave de sesión AES:", texto_claro) # Se calcula el hash SHA-256 (256 bits) del texto en claro descifrado, # es decir, su firma digital, para compararla después con la firma digital # recibida que se descifra a continuación. h = (hashlib.sha256(texto_claro.encode()).digest()) print ("[+] Firma digital calculada para el texto en claro descifrado (hexadecimal):", h.hex()) # Se lee la clave pública del emisor, el módulo (n) y el exponente de # la clave pública (e), para descifrar la firma digital. datos_clave_publica = clave_rsa("public_emisor.pem") print ("[+] Clave pública del emisor:") print (" Módulo (n):", datos_clave_publica.n) print (" Exponente clave pública (e):", datos_clave_publica.e) # Se descifra la firma digital correspondiente al texto en claro que se ha # recibido con la clave pública del emisor (criptografía asimétrica). firma_digital = exp_modular_rapida(int(b64decode(datos_comunicacion[2])), datos_clave_publica.e, datos_clave_publica.n) print ("[+] Firma digital correspondiente al texto en claro que se ha recibido (hexadecimal):", hex(firma_digital)[2:]) if hex(firma_digital)[2:] == h.hex(): print ("[+] Se ha verificado la firma digital del contenido de la comunicación con el resultado de FIRMA DIGITAL VÁLIDA.") else: print ("[+] Se ha verificado la firma digital del contenido de la comunicación con el resultado de FIRMA DIGITAL NO VÁLIDA.") elif opcion == "2": print ("*** FIN ******************************************") salir = True else: print ("*** ERROR: Opción no válida.") if __name__ == '__main__': main()
Lo ejecuto:
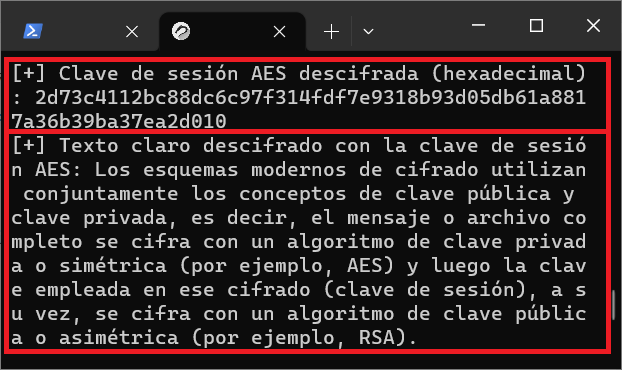
Tras leerse del fichero que simula la comunicación, comunicacion.txt: la clave de sesión cifrada, el criptograma o texto en claro cifrado y la firma digital cifrada, lo primero que hace el script es descifrar la clave de sesión AES con la clave privada del receptor (criptografía asimétrica) y descifrar el texto en claro cifrado con ella por el emisor (criptografía simétrica). Para optimizar el consumo de tiempo y recursos en este descifrado el script utiliza el Teorema Chino del Resto (TCR o CRT por sus siglas en inglés, 'Chinese Remainder Theorem').
Lo siguiente que hace el script es calcular el hash SHA-256 del texto en claro descifrado, para compararlo con la firma digital que se descifra justo después.
Y, finalmente, el script lee la clave pública del emisor (módulo y exponente de la clave pública) para descifrar mediante el algoritmo RSA (criptografía asimétrica) la firma digital cifrada que se ha recibido, y compara ésta con la obtenida en el punto anterior.
Tal y como se puede observar en la figura anterior, en este caso el proceso de verificación de la firma digital termina con éxito y, por tanto, quedarían acreditadas tanto la autenticidad como la integridad del mensaje recibido.
Quizás también te interese:





.png)
.png)

Comentarios
Publicar un comentario