Gimnasia mental (XXIV): La pregunta más difícil en una entrevista de trabajo

Esta semana diversos medios de comunicación online publicaban un artículo con el título "La pregunta más difícil formulada en una entrevista de trabajo", en donde se nos contaba que, al final de la entrevista, el entrevistador formulaba una última pregunta al entrevistado:

"Un triángulo rectángulo tiene una hipotenusa que mide 10 cm y una altura de 6 cm. Calcule el área del triángulo".

Pregunta a la que el entrevistado respondió que el área de dicho triángulo era 30 cm2. (S = base x altura / 2 = 10 x 6 / 2 = 30).

Evidentemente, ésta no es la respuesta correcta (aunque yo hubiera respondido lo mismo), pero la pregunta así formulada creo que puede ser equívoca. ¿Por qué digo esto?

Porque todo triángulo tiene 3 alturas (el segmento perpendicular a cada uno de sus tres lados que va desde el vértice opuesto a cada uno de ellos o a su prolongación).

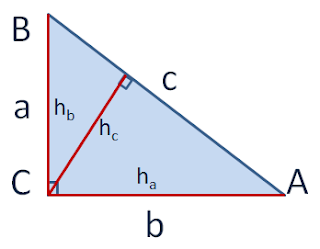
Pensemos en un triángulo rectángulo:

Y, por tanto, hay tres alturas (ha, hb y hc) según a qué lado esté asociada cada una de ellas. En un triángulo rectángulo las alturas relativas a cada cateto coinciden con la longitud del otro cateto (ha = b; hb = a), mientras que la altura relativa a la hipotenusa sería igual al producto de ambos catetos dividido entre la hipotenusa (hc = a x b / c).

Con la pregunta así formulada, sin indicarse a qué altura se refiere, podríamos pensar que se trata de un triángulo rectángulo con la altura relativa a uno de los catetos igual a 6 (hb = a = 6), es decir:

Y, por tanto que el Área que se nos pide calcular es 24 cm2. (S = base x altura / 2 = 8 x 6 / 2 = 24).

Sin embargo, en la web Quora.com, donde se cuenta esta pequeña historia, se ve que en la pregunta formulada en inglés queda claro que el entrevistador se refería a la altura relativa a la hipotenusa: "A right triangle has a hypotenuse equal to 10 and an altitude to the hypotenuse equal to 6. Find the area of the triangle", por lo que no se trata del triángulo anterior, sino del siguiente:

¿Cuál es el área del triángulo en este caso? Pues ninguna, porque simplemente este triángulo rectángulo no existe, ya que la altura máxima relativa a la hipotenusa de un triángulo rectángulo de hipotenusa 10 es 5 (nunca puede superar la mitad de la hipotenusa) y, por tanto, el área máxima de un triángulo rectángulo de hipotenusa 10 cm es 25 cm2. (S = base x altura / 2 = 10 x 5 / 2 = 25).

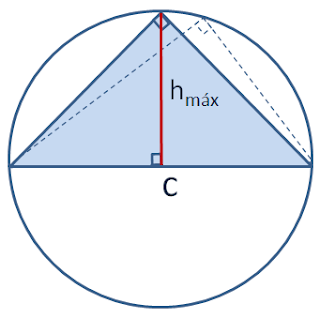
Esto es fácilmente demostrable si inscribimos un triángulo rectángulo en una circunferencia de diámetro igual a la hipotenusa:

De esta forma los dos ángulos agudos sumarán 90o y el ángulo recto será el correspondiente al vértice opuesto a la hipotenusa (el diámetro de la circunferencia). Como se puede observar en la figura anterior la altura máxima (hmáx se alcanzará cuando h_c sea igual al radio de la circunferencia, o lo que es lo mismo la mitad de la hipotenusa (c), triángulo rectángulo isósceles. En nuestro caso: hmáx =  5, por lo que el triángulo rectángulo de la pregunta no puede existir, al menos en geometría euclídea plana.