La pequeña historia del Ajedrez (III)

Los problemas de Ajedrez son muy antiguos, los maestros árabes ya componían problemas de Shatranj hace muchos siglos, y han contribuido de forma decisiva a difundir este juego.

Antes de poner algunos ejemplos de problemas famosos en los siguientes posts de esta serie, e incluso de partidas o posiciones célebres, tenemos que hablar de la notación algebraica, que es la notación oficial que se utiliza para representar por escrito la secuencia de los movimientos del Ajedrez.

En esta notación se utiliza una letra mayúscula para identificar a las piezas del tablero (en castellano, las siguientes):

Es decir, cada una de las piezas (excepto el peón, que no tiene asociada ninguna letra) se identifica por la letra mayúscula correspondiente a la inicial de su nombre, en castellano: (C)aballo, (A)lfil, (T)orre, (D)ama y (R)ey.

Cada una de las casillas o escaques es identificada de manera inequívoca por la intersección de una letra (de la 'a' a la 'h') y de un dígito (del '1' al '8').

Para ello, en las columnas se colocan dichas letras, de izquierda a derecha, y en las filas los dígitos (en orden ascendente comenzando por la primera fila correspondiente al jugador que juega con las piezas blancas, que se sitúan siempre en la parte inferior del tablero).

Las letras que identifican a las piezas se escriben en mayúsculas y las correspondientes a las columnas en minúsculas.

Un movimiento básico se describe por la letra de la pieza que se mueve (sin letra para el peón) seguida por la identificación de la casilla destino o a la que se mueve (letra de la columna y dígito de la fila).

Ejemplos:

Un movimiento de captura se describe por la letra de la pieza que se mueve o captura (si es un peón por la letra de la columna en la que se encuentra) seguida por el carácter `x' e, igual que en el movimiento básico, por la identificación de la casilla destino o en la que se encuentra la pieza a capturar (letra de la columna y dígito de la fila).

Ejemplos:

En el caso de ambigüedades, es decir, que dos piezas del mismo tipo se puedan mover a la misma casilla destino, estas se resuelven insertando la letra de la columna en la que se halla la pieza a mover después de la letra que la identifica.

O, en el caso de que ambas piezas estén situadas en la misma columna, insertando el dígito de la fila en la que se encuentra la pieza a mover después de la letra que la identifica.

Ejemplos:

El enroque corto (lado del rey) se representa mediante 0-0, mientras que el enroque largo (lado de la dama) se representa mediante 0-0-0.

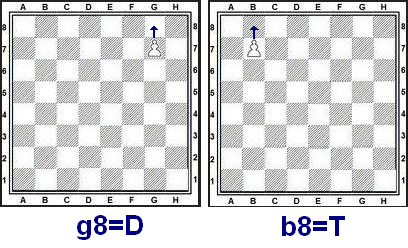
La promoción de un peón al alcanzar la octava fila se representa mediante la identificación de la casilla destino, es decir, en la que promociona el peón, seguida del carácter '=' y de la letra que identifica a la pieza a la que promociona.

Ejemplos:

Por último, si un movimiento provoca jaque se indica con el carácter '+' inmediatamente después del movimiento, mientras que para el jaque mate se utiliza '++' o '#'.    

Ejemplos: